| 1.1. | Η έννοια της μεταβλητής - Aλγεβρικές παραστάσεις |
|
Μεταβλητή
ΛύσηΕύκολα βέβαια βρίσκουμε ότι:
Μπορούμε λοιπόν να σκεφτούμε ότι το κόστος ενός τηλεφωνήματος θα είναι: (διάρκεια τηλεφωνήματος) · 0,005 €. Για ευκολία, συμβολίζουμε με το γράμμα x τη διάρκεια του τηλεφωνήματος (σε δευτερόλεπτα), οπότε καταλήγουμε ότι το κόστος για κάθε τηλεφώνημα διάρκειας x δευτερολέπτων είναι: x · 0,005 €. To γράμμα x που παριστάνει έναν οποιοδήποτε αριθμό, λέγεται μεταβλητή. Φυσικά, μπορούμε να χρησιμοποιήσουμε και άλλα γράμματα (ελληνικά ή λατινικά) για να παραστήσουμε μεταβλητές: y, z, t, α, β, γ, ... Αλγεβρικές παραστάσεις - Αναγωγή ομοίων όρων
ΛύσηΓια να βρούμε το εμβαδόν του μεγάλου ορθογωνίου, υπάρχουν δύο τρόποι:
Φυσικά, και οι δύο τρόποι θα πρέπει να δίνουν το ίδιο αποτέλεσμα, δηλαδή: (α + β) · γ = α · γ + β · γ, που είναι η γνωστή επιμεριστική ιδιότητα, η οποία μπορεί να γραφεί και στη μορφή:
Στη μορφή αυτή, η επιμεριστική ιδιότητα μπορεί να μας βοηθήσει να κάνουμε εύκολα πράξεις στις αλγεβρικές παραστάσεις: Παράδειγμα:7 · α + 8 · α = (7 + 8) · α = 15 · α
Η διαδικασία αυτή με την οποία γράψαμε σε απλούστερη μορφή τις παραπάνω αλγεβρικές παραστάσεις, ονομάζεται «αναγωγή ομοίων όρων». |
Παρατήρηση:Όταν γράφουμε αλγεβρικές παραστάσεις, συνήθως δε βάζουμε το σύμβολο (·) του πολλαπλασιασμού μεταξύ των αριθμών και των μεταβλητών ή μεταξύ των μεταβλητών. Γράφουμε δηλαδή 3xy αντί για 3·x·y. Eπίσης, γράφουμε 2(4xy – 1) + 3(2 – 5x) αντί για 2 ·( 4· x· y – 1) + 3 ·( 2 – 5 · x ). To σύμβολο του πολλαπλασιασμού θα χρησιμοποιείται βέβαια, για τον πολλαπλασιασμό αριθμών: 3 · 5 ή 3·(–5).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


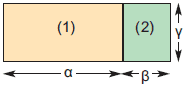
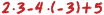 είναι μια αριθμητική παράσταση. Ομοίως, η παράσταση
είναι μια αριθμητική παράσταση. Ομοίως, η παράσταση 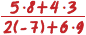 είναι μία αριθμητική παράσταση.
είναι μία αριθμητική παράσταση.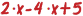 είναι μια αλγεβρική παράσταση. Oι προσθετέοι λέγονται όροι αυτής. Ομοίως, η παράσταση
είναι μια αλγεβρική παράσταση. Oι προσθετέοι λέγονται όροι αυτής. Ομοίως, η παράσταση 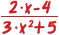 είναι μία αλγεβρική παράσταση. Πώς κάνουμε όμως τις πράξεις σε μια αλγεβρική παράσταση; Στο σημείο αυτό μπορεί να μας βοηθήσει λίγο η Γεωμετρία! Ας θυμηθούμε, λοιπόν, τα εμβαδά των ορθογωνίων:
είναι μία αλγεβρική παράσταση. Πώς κάνουμε όμως τις πράξεις σε μια αλγεβρική παράσταση; Στο σημείο αυτό μπορεί να μας βοηθήσει λίγο η Γεωμετρία! Ας θυμηθούμε, λοιπόν, τα εμβαδά των ορθογωνίων: