B1.2: Μονάδες μέτρησης επιφανειών

1.2.	Μονάδες μέτρησης επιφανειών

	Ας θεωρήσουμε ένα τετράγωνο πλευράς 1 m. Το εμβαδόν του τετραγώνου αυτού λέγεται τετραγωνικό μέτρο (1 m²) και το χρησιμοποιούμε ως μονάδα μέτρησης εμβαδών.
	Αφού 1 m = 10 dm, το τετραγωνικό μέτρο χωρίζεται σε 10 • 10 = 100 «τετραγωνάκια» πλευράς 1 dm. To εμβαδόν σε κάθε τετραγωνάκι ονομάζεται τετραγωνικό δεκατόμετρο ή τετραγωνική παλάμη (1 dm²). Παρατηρούμε ότι 1 m² = 100 dm².
	Ας θεωρήσουμε τώρα ένα τετράγωνο πλευράς 1 dm. Αφού 1 dm = 10 cm, το τετραγωνικό δεκατόμετρο χωρίζεται σε 10 • 10 = 100 «τετραγωνάκια» πλευράς 1 cm. Το εμβαδόν ενός τετραγώνου πλευράς 1 cm λέγεται τετραγωνικό εκατοστόμετρο ή τετραγωνικός πόντος (1 cm²). Παρατηρούμε ότι 1 dm² = 100 cm².
	Ας θεωρήσουμε τώρα ένα τετράγωνο πλευράς 1 cm. Αφού 1 cm = 10 mm, το τετραγωνικό εκατοστόμετρο χωρίζεται σε 10 • 10 = 100 «τετραγωνάκια» πλευράς 1 mm. Το εμβαδόν ενός τετραγώνου πλευράς 1 mm λέγεται τετραγωνικό χιλιοστόμετρο (1 mm²). Παρατηρούμε ότι 1 cm² = 100 mm².
	Άλλες μονάδες μέτρησης εμβαδών είναι: Το τετραγωνικό χιλιόμετρο (1 km²), το οποίο ισούται με το εμβαδόν ενός τετραγώνου πλευράς 1000 m. Επομένως 1 km² = 1000 • 1000 = 1.000.000 m². Χρησιμοποιείται κυρίως για τη μέτρηση μεγάλων εκτάσεων, όπως είναι η έκταση που καταλαμβάνει ένα κράτος, ένας νομός ή ένα νησί. Το στρέμμα, το οποίο ισούται με 1000 m² και χρησιμοποιείται κυρίως για τη μέτρηση των εμβαδών οικοπέδων και κτημάτων.

Συνοψίζοντας τα παραπάνω σχηματίζουμε τον πίνακα:

1 m² =	100 dm² =	10.000 cm² =	1.000.000 mm²
	1 dm² =	100 cm² =	10.000 mm²
		1 cm² =	100 mm²

1 mm² =	0,01 cm² =	0,0001 dm² =	0,000001 m²
	1 cm² =	0,01 dm² =	0,0001 m²
		1 dm² =	0,01 m²

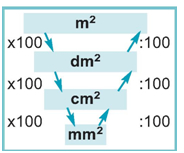
Mε τη βοήθεια του σχήματος μετατροπής μονάδων εμβαδού,

να συμπληρώσετε τον διπλανό πίνακα.

m²	dm²	cm²	mm²
253
	320
		7122
			12653

Λύση:

Σύμφωνα με το παραπάνω σχήμα, για να μετατρέψουμε ένα εμβαδόν στην αμέσως μικρότερη μονάδα, πολλαπλασιάζουμε με το 100, ενώ για να το μετατρέψουμε στην αμέσως μεγαλύτερη μονάδα, διαιρούμε με το 100.

Επομένως:

m²	dm²	cm²	mm²
253	25300	2530000	253000000
3,20	320	32000	3200000
0,7122	71,22	7122	712200
0,012653	1,2653	126,53	12653

Να βάλετε σε αύξουσα σειρά τα παρακάτω εμβαδά:

α) 3,7 dm², 7 cm², 4,3 cm², 3,7 m².

β) 40 cm², 42 mm², 40 dm², 3 m².

γ) 1453 mm², 14,5 cm², 1,4 dm², 0,14 m².

Λύση:

α) Μετατρέπουμε τα τέσσερα εμβαδά στην ίδια μονάδα μέτρησης:

3,7 dm² = 370 cm², 3,7 m² = 37000 cm², οπότε:

4,3 cm² < 7 cm² < 3,7 dm² = 370 cm² < 3,7 m² = 37000 cm².

β) 42 mm² < 40 cm² = 4000 mm² < 40 dm² = 400000 mm² <3 m² = 3000000 mm²

γ) Αφού 14,5 cm² = 1450 mm², 1,4 dm² = 14000 mm² και 0,14 m² = 140000mm²,

έχουμε ότι: 14,5 cm² < 1453 mm² < 1,4 dm² < 0,14 m².

1.	Nα επιλέξετε τη σωστή απάντηση.

		Α	Β	Γ	Δ
1	6,2 m² =	62 cm²	620 cm²	62000 cm²	0,62 cm²
2	6,2 mm² =	62 cm²	620 cm²	0,62 cm²	0,062 cm²
3	6,2 cm² =	62 m²	0,62 m²	620 m²	0,00062 m²
4	6,2 cm² =	620 mm²	6200 mm²	0,62 mm²	0,00062 mm²
5	6,2 m² =	62 dm²	620 dm²	62000 dm²	0,062 dm²
6	6,2 mm² =	0,0000062 m²	0,00062 m²	0,062 m²	0,0062 m²

2.	Να επιλέξετε τη σωστή απάντηση. Για να μετατρέψουμε:

	Α	Β	Γ
1. m² σε dm²	πολλαπλασιάζουμε με 100	διαιρούμε με 100	διαιρούμε με 10
2. dm² σε cm²	διαιρούμε με 100	πολλαπλασιάζουμε με 100	διαιρούμε με 10
3. cm² σε mm²	διαιρούμε με 100	διαιρούμε με 10	πολ/με με 100
4. dm² σε m²	πολλαπλασιάζουμε με 100	διαιρούμε με 100	διαιρούμε με 10
5. cm² σε dm²	πολλαπλασιάζουμε με 10.000	πολλαπλασιάζουμε με 100	διαιρούμε με 100
6. mm² σε cm²	διαιρούμε με 100	πολλαπλασιάζουμε με 100	διαιρούμε με 10
7. m² σε cm²	διαιρούμε με 100	πολλαπλασιάζουμε με 10.000	διαιρούμε με 10.000
8. m² σε mm²	πολ/με με 1.000.000	διαιρούμε με 100.000	διαιρούμε με 1.000
9. cm² σε m²	διαιρούμε με 100	διαιρούμε με 10.000	πολ/με με 10.000
10. mm² σε dm²	διαιρούμε με 100	πολλαπλασιάζουμε με 10.000	διαιρούμε με 10.000

1.	Να μετατρέψετε σε m² τα παρακάτω μεγέθη: 32 cm², 312 cm², 127 km², 710 dm², 12720 mm², 212 dm², 1280 mm², 79 km².
2.	Να μετατρέψετε σε cm² τα παρακάτω μεγέθη: 12 m², 175 dm², 456 m², 136 m², 3 km², 1750 mm², 256 km².
3.	Να μετατρέψετε σε mm² τα παρακάτω μεγέθη: 12 km², 431 m², 17 dm², 236 cm².
4.	Να μετατρέψετε σε km² τα παρακάτω μεγέθη: 7233 mm², 4321 cm², 6322 dm², 14632 mm², 560 m².

Στις παρακάτω περιπτώσεις να εκφράσετε τα εμβαδά στην ίδια μονάδα μέτρησης και στη συνέχεια να τις κατατάξετε κατά σειρά μεγέθους από το μικρότερο προς το μεγαλύτερο.

α) 13850 mm², 0,23 m², 0,48 m², 670 cm²,

13,7 dm².

β) 32 dm², 1,23 m², 23270 mm², 1356 cm².

Ποια από τις μονάδες μέτρησης εμβαδού θα πρέπει να χρησιμοποιήσουμε, για να μετρήσουμε το εμβαδόν:

α) του δωματίου μας,

β) της Κρήτης,

γ) ενός αγρού,

δ) ενός γραμματόσημου,

ε) ενός φύλλου τετραδίου.