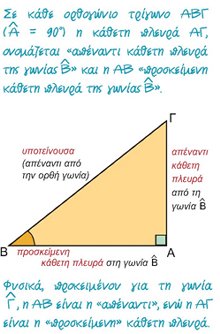
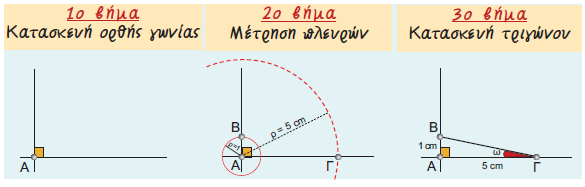
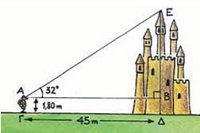
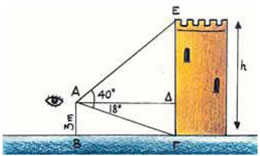
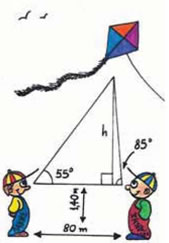
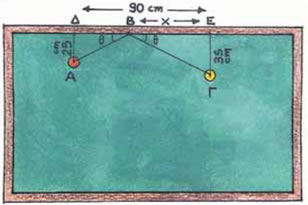
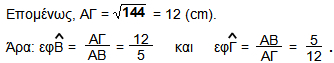2.1. Εφαπτομένη οξείας γωνίας

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

Η πινακίδα που βρίσκεται στο σημείο Ο πληροφορεί τον οδηγό του αυτοκινήτου πόσο ανηφορικός είναι ο δρόμος ΟΓ.

Το ποσοστό 10% ή σημαίνει ότι σε κάθε 100 m οριζόντιας απόστασης ανεβαίνουμε 10m.

Έτσι, π.χ. στο σημείο Α είναι ΟΑ = 50 m και ανεβαίνουμε ΑΔ = 50 • 0,1 m = 5 m.

Να συμπληρώσετε τον παρακάτω πίνακα:

Τι παρατηρείτε;

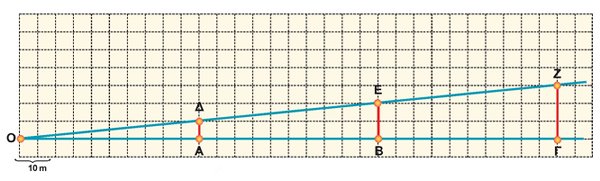
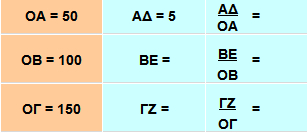
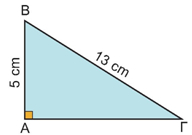
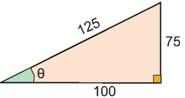
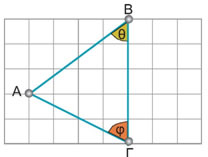
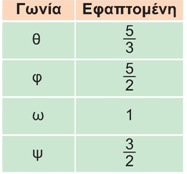
Λύση

Παρατηρούμε ότι ΒΕ = 10, ΓΖ = 15, οπότε οι λόγοι της τρίτης στήλης παραμένουν σταθεροί:

 

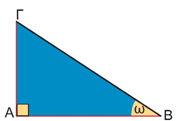
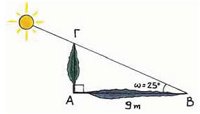
Αν ονομάσουμε ω τη γωνία που σχηματίζει ο ανηφορικός δρόμος με το οριζόντιο επίπεδο, τότε οι λόγοι

 και γενικά ο λόγος είναι ο ίδιος για όλα τα σημεία της

ευθείας ΟΖ. Ο σταθερός αυτός λόγος λέγεται εφαπτομένη της γωνίας ω και γράφουμε εφω = 0,1.

Ειδικά, όταν αναφερόμαστε σε δρόμο, όπως παραπάνω, η εφαπτομένη της γωνίας ω ονομάζεται κλίση του δρόμου.

Σε οποιοδήποτε ορθογώνιο τρίγωνο με οξεία γωνία ω ο σταθερός αυτός λόγος γράφεται ως εξής:

 

 

ονομάζεται εφαπτομένη της γωνίας ω και συμβολίζεται με εφω.

 

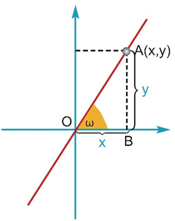
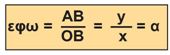
Ο λόγος που σχηματίζεται, αν διαιρέσουμε την απέναντι κάθετη πλευρά με την προσκείμενη κάθετη πλευρά μιας οξείας γωνίας ω ενός ορθογωνίου τριγώνου, είναι πάντοτε σταθερός και λέγεται εφαπτομένη της γωνίας ω.

 

Σχόλιο 1:

Ας θυμηθούμε την κλίση της ευθείας με εξίσωση y = αx, που συναντήσαμε στην παράγραφο 3.3.

Είδαμε ότι o λόγος είναι πάντα σταθερός και ίσος με τον αριθμό α για κάθε σημείο Α της ευθείας

με εξίσωση y = αx.

Αν ω είναι η γωνία που σχηματίζει η ευθεία με εξίσωση y = αx με τον άξονα x'x, τότε στο ορθογώνιο τρίγωνο ΟΑΒ ισχύει:

 

 

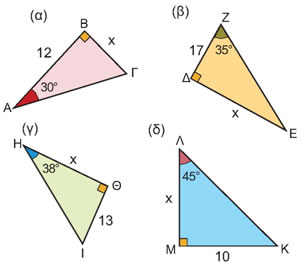
Η κλίση α της ευθείας με εξίσωση y = αx είναι ίση με την εφαπτομένη της γωνίας ω, που σχηματίζει η ευθεία με τον άξονα x'x.

 

Σχόλιο 2:

Για να υπολογίσουμε την εφαπτομένη μιας γωνίας, μπορούμε να χρησιμοποιήσουμε τον πίνακα τριγωνομετρικών αριθμών των γωνιών 1° - 89°, που βρίσκεται στο τέλος του βιβλίου (σελ. 254).

Σε επόμενη παράγραφο (§2.3) θα μάθουμε να υπολογίζουμε την εφαπτομένη μιας γωνίας χρησιμοποιώντας έναν «επιστημονικό» υπολογιστή τσέπης.

 
1

Δίνεται ορθογώνιο τρίγωνο ΑΒΓ με υποτείνουσα ΒΓ = 13 cm. Αν η μία κάθετη πλευρά έχει μήκος ΑΒ = 5 cm, να υπολογίσετε τις εφαπτομένες των γωνιών .

 

Λύση:

Γνωρίζουμε ότι:

Επομένως, πρέπει πρώτα να υπολογίσουμε το μήκος της κάθετης πλευράς ΑΓ.

Από το Πυθαγόρειο θεώρημα γνωρίζουμε ότι ΑΒ² + ΑΓ² = ΒΓ² και αντικαθιστώντας με ΑΒ = 5 cm και ΒΓ = 13 cm,

έχουμε: 5² + ΑΓ² = 13²   ή   25 + ΑΓ² = 169    ή   ΑΓ² = 169 - 25 = 144

 

 

2

Να σχεδιάσετε μια γωνία ω, με

 

Λύση:

Σύμφωνα με τον ορισμό της εφαπτομένης οξείας γωνίας ορθογωνίου τριγώνου, ισχύει:

 

Επομένως, για να σχεδιάσουμε μια οξεία γωνία ω με αρκεί να κατασκευάσουμε ένα ορθογώνιο τρίγωνο που η μία κάθετη πλευρά του θα είναι ίση με 1 και η άλλη κάθετη πλευρά ίση με 5.

Για τη γωνία ω ισχύει:

 

3

Να υπολογίσετε το ύψος του κυπαρισσιού του παρακάτω σχήματος χρησιμοποιώντας το μήκος της σκιάς του και τη γωνία ω.

 

Λύση:

Στο ορθογώνιο τρίγωνο ΑΒΓ γνωρίζουμε ότι ΑΒ = 9 m και

Θέλουμε να υπολογίσουμε την πλευρά ΑΓ.

Ο τριγωνομετρικός αριθμός που συνδέει την απέναντι με την προσκείμενη πλευρά μιας γωνίας ενός

ορθογωνίου τριγώνου ΑΒΓ είναι η εφαπτομένη της γωνίας .

Έχουμε λοιπόν:

οπότε

Με τη βοήθεια του πίνακα εφαπτομένων βρίσκουμε ότι εφ25° = 0,47.

Άρα, ΑΓ = 9 • 0,47 = 4,23, δηλαδή το ύψος του κυπαρισσιού είναι 4,23 m.

 

4

Ένας τουρίστας ύψους ΑΓ = 1,80 m «βλέπει» τον πύργο με γωνία 32° και απέχει από αυτόν 45 m. Να υπολογίσετε το ύψος ΕΔ του πύργου.

 

Λύση:

Στο ορθογώνιο τρίγωνο ΑΒΕ γνωρίζουμε το μήκος της κάθετης πλευράς ΑΒ = 45 m και μια οξεία γωνία 32°. Επομένως, για να υπολογίσουμε την άλλη κάθετη πλευρά ΒΕ, χρησιμοποιούμε την εφαπτομένη της γωνίας των 32°.

 

 

Επομένως, το συνολικό ύψος του πύργου είναι: ΔΕ = ΔΒ + ΒΕ = 1,8 + 27,9 = 29,7 (m).

 

 

 1.

Στο διπλανό σχήμα είναι εφθ =......................

 

Να κυκλώσετε τη σωστή απάντηση.

 2.

Στο διπλανό σχήμα είναι:

α) εφθ = ......................

α) εφφ = ......................

Να κυκλώσετε τη σωστή απάντηση.

 3.

Σε κάθε γωνία θ, φ, ω, ψ του διπλανού σχήματος να αντιστοιχίσετε την εφαπτομένη της.

 

 

 

 1.

Στα παρακάτω σχήματα να υπολογίσετε το μήκος x :

 2.

Να σχεδιάσετε μια γωνία ω με εφω = 0,7.

 3.

Ποια στοιχεία μπορείτε να υπολογίσετε σε ορθογώνιο τρίγωνο με μια

οξεία γωνία 30°, αν η απέναντι κάθετη πλευρά έχει μήκος 4 cm;

 4.

Στο παρακάτω σχήμα να υπολογίσετε την απόσταση των δύο πλοίων.

 5.

Ένας τουρίστας βλέπει την κορυφή ενός πύργου από σημείο Α με γωνία 40° και τη βάση του πύργου με γωνία 18°. Αν γνωρίζετε ότι ΑΒ = 3 m, να υπολογίσετε το ύψος h του πύργου.

 

 6.

Την Καθαρά Δευτέρα ο Λάκης και ο Σάκης βλέπουν το χαρταετό του Μάκη με γωνίες 55° και 85° αντίστοιχα. Ο Λάκης και ο Σάκης βρίσκονται σε απόσταση 80 m.

Να βρείτε σε τι ύψος από το έδαφος έχει ανέβει ο χαρταετός του Μάκη, αν γνωρίζουμε ότι τα μάτια του Λάκη και του Σάκη βρίσκονται σε ύψος 1,40 m.

 7.

Στο παρακάτω σχήμα βλέπουμε ένα τραπέζι του μπιλιάρδου. Δύο μπάλες Α και Γ είναι τοποθετημένες έτσι ώστε, ΔΕ = 90 cm, ΑΔ = 25 cm, ΓΕ = 35 cm και ΒΕ = x cm. Ένας παίκτης θέλει να χτυπήσει τη μπάλα Γ με τη μπάλα Α ακολουθώντας τη διαδρομή ΑΒΓ του σχήματος.

α) Να εκφράσετε την απόσταση ΒΔ ως συνάρτηση του χ.

β) Στο τρίγωνο ΑΔΒ να εκφράσετε την εφθ ως συνάρτηση του x.

γ) Στο τρίγωνο ΒΕΓ να εκφράσετε την εφθ ως συνάρτηση του x.

δ) Χρησιμοποιώντας τα παραπάνω συμπεράσματα των ερωτημάτων

(β) και (γ), να αποδείξετε ότι το χ είναι λύση της εξίσωσης 35(90–x) = 25x.

Να προσδιορίσετε τον αριθμό x.