2.3. Μεταβολές ημιτόνου, συνημιτόνου και εφαπτομένης

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Η χρήση του υπολογιστή τσέπης για τον υπολογισμό του ημιτόνου, του συνημιτόνου και της εφαπτομένης μιας γωνίας ω

Επειδή ο υπολογισμός του ημιτόνου, συνημιτόνου και εφαπτομένης μιας γωνίας δεν είναι απλός, χρησιμοποιούμε συχνά έναν «επιστημονικό» υπολογιστή τσέπης. Ο «επιστημονικός» υπολογιστής περιλαμβάνει τα πλήκτρα

 

 

To πρώτο υπολογίζει το ημίτονο, το δεύτερο το συνημίτονο και το τρίτο την εφαπτομένη μίας γωνίας (π.χ. των 63°) ως εξής:

α) Πατάμε το πλήκτρο που μετατρέπει τους αριθμούς σε μοίρες. Το πλήκτρο αυτό διαφέρει από υπολογιστή σε υπολογιστή. Συνήθως η ένδειξη που φανερώνει ότι έχουμε πατήσει το σωστό πλήκτρο είναι DEG.

β) Πατάμε διαδοχικά τα πλήκτρα:

γ) Στην οθόνη παρουσιάζεται ο αριθμός 0,891 που είναι το ημ63°.

δ) Ανάλογα πατώντας τα πλήκτρα:

 

Παρατήρηση:

Στο τέλος του βιβλίου (σελ. 254) μπορείτε να βρείτε έναν πίνακα με τους τριγωνομετρικούς αριθμούς των γωνιών από 1° έως 89°, για να τον χρησιμοποιήσετε στις ασκήσεις.

 

Μεταβολές ημιτόνου, συνημιτόνου και εφαπτομένης
οξείας γωνίας ω

Ας εξετάσουμε τώρα τι συμβαίνει όταν μεταβάλλεται η γωνία ω ενός ορθογωνίου τριγώνου.

 

1

Χρησιμοποιώντας έναν υπολογιστή τσέπης ή τον πίνακα των τριγωνομετρικών αριθμών που βρίσκεται στο τέλος του βιβλίου, να συμπληρώσετε τον παρακάτω πίνακα:

Λύση

Bρίσκουμε ότι:

 

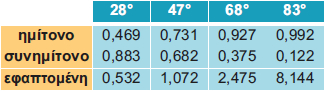
Από τον προηγούμενο πίνακα παρατηρούμε ότι:

 

Όταν μια οξεία γωνία αυξάνεται, τότε: αυξάνεται το ημίτονό της, ελαττώνεται το συνημίτονό της και αυξάνεται η εφαπτομένη της.

 

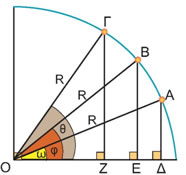
Γεωμετρικά, τα παραπάνω συμπεράσματα φαίνονται στα διπλανά σχήματα:

Σχηματίζουμε τα ορθογώνια τρίγωνα ΟΑΔ, ΟΒΕ, ΟΓΖ, με σταθερή υποτείνουσα R = ΟΑ = ΟΒ = ΟΓ και θεωρούμε τρεις γωνίες: ω < φ < θ.

Παρατηρούμε ότι: ΑΔ < ΒΕ < ΓΖ.

Επομένως, διαιρώντας με R έχουμε ότι:

Στο ίδιο σχήμα παρατηρούμε ότι: ΟΔ > ΟΕ > ΟΖ. Οπότε:

 

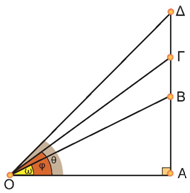
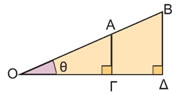
Ας θεωρήσουμε ορθογώνια τρίγωνα ΟΑΒ, ΟΑΓ, ΟΑΔ με σταθερή τη μία κάθετη πλευρά ΟΑ και ορθή τη γωνία

Παρατηρούμε ότι, όταν η οξεία γωνία με κορυφή το σημείο Ο μεγαλώνει, δηλαδή: ω < φ < θ, τότε μεγαλώνει αντίστοιχα η απέναντι κάθετη πλευρά: ΑΒ < ΑΓ < ΑΔ. Επομένως:

Από τα παραπάνω προκύπτει ότι:

 

Αν δύο οξείες γωνίες έχουν ίσα ημίτονα, τότε οι γωνίες αυτές είναι ίσες.
Αν δύο οξείες γωνίες έχουν ίσα συνημίτονα, τότε οι γωνίες αυτές είναι ίσες.
Αν δύο οξείες γωνίες έχουν ίσες εφαπτομένες, τότε οι γωνίες αυτές είναι ίσες.

 
1

Στο διπλανό σχήμα είναι ΟΑ = 5 cm, OB = 8 cm και ΑΓ = 2 cm. Να υπολογίσετε την απόσταση ΒΔ.

 

Λύση:

Παρατηρούμε ότι στο σχήμα υπάρχουν δύο ορθογώνια τρίγωνα, τα ΟΑΓ και ΟΒΔ με κοινή γωνία θ.

 

2

Το ημίτονο της γωνίας που σχηματίζει μια πίστα του σκι με το οριζόντιο επίπεδο είναι

Αν ένας σκιέρ βρίσκεται σε σημείο Γ ύψους ΑΓ = 155 m από το έδαφος, να βρεθεί η απόσταση ΒΓ που θα διανύσει ο σκιέρ ώσπου να φτάσει στο έδαφος.

 

Λύση:

 

3

Ένας παρατηρητής Α, που βρίσκεται 100 m από την ακτή Β και 150 m από ένα δέντρο Γ, θέλει να υπολογίσει την απόσταση ΒΔ του πλοίου Δ από την ακτή Β. Μ’ ένα γωνιόμετρο (ένα όργανο που μας επιτρέπει να μετράμε γωνίες) σκοπεύει το πλοίο και το δέντρο και βρίσκει τη γωνία

Αν να υπολογίσετε την απόσταση ΔΒ.

 

Λύση:

Έστω x = ΒΔ η απόσταση του πλοίου από την ακτή. Στο ορθογώνιο τρίγωνο ΑΓΔ χρησιμοποιούμε το συνημίτονο της γωνίας των 70°.

 

 

 

 1.

Να κυκλώσετε τις σωστές απαντήσεις που αφορούν τις γωνίες των διπλανών ορθογωνίων τριγώνων:

α) A: φ < θ     B: φ = θ     Γ: φ > θ

β) A: ω < y      B: ω = y     Γ: ω > y

 2.

Να χαρακτηρίσετε τις παρακάτω προτάσεις με Σ (σωστό) ή Λ (λανθασμένο).

 

α) ημ13° <ημ15°

β)συν13°< συν15°

γ) συν57° < συν27°

δ) ημ57° < ημ27°

ε) ημ32° < ημ23°

στ) συν32° < συν23°

 

 

 1.

Να υπολογίσετε το χ σε καθένα από τα παρακάτω τρίγωνα:

 2.

Να υπολογίσετε το χ στα παρακάτω τρίγωνα:

 3.

Σ' ένα ιστιοπλοϊκό σκάφος το ύψος του καταρτιού έως το σημείο Α είναι 8 m. Να βρείτε το μήκος που έχουν τα συρματόσχοινα που στηρίζουν τα πανιά, αν αυτά σχηματίζουν γωνίες 55° και 70° αντίστοιχα με το επίπεδο της θάλασσας.

 4.

Ένας μηχανικός θέλει να κατασκευάσει ένα σπίτι με υπόγειο γκαράζ. Το ύψος του γκαράζ πρέπει να είναι ΒΓ = 2,25 m και η κλίση της ράμπας θ = 13°. Να βρείτε το μήκος ΑΓ της ράμπας και την απόσταση ΑΒ του σημείου Α από το σπίτι.

 5.

Να διατάξετε από τον μεγαλύτερο στον μικρότερο τους τριγωνομετρικούς αριθμούς (χωρίς να τους υπολογίσετε):

α) ημ37°, ημ56°, ημ16° και ημ20°

β) συν25°, συν36°, συν20° και συν28°

γ) εφ18°, εφ22°, εφ51° και εφ89°

 6.

Μια σκάλα ύψους 6 m είναι ακουμπισμένη σε τοίχο ύψους 7 m. Για λόγους ασφαλείας, η γωνία στο έδαφος πρέπει να είναι 75°. Να βρείτε την απόσταση ΑΒ όπου πρέπει να τοποθετηθεί η βάση της σκάλας από τον τοίχο, καθώς και την απόσταση ΓΔ από το πάνω μέρος της σκάλας έως το πάνω μέρος του τοίχου.

 7.

Ένας γεωλόγος θέλει να υπολογίσει την απόσταση από το σημείο Α, όπου βρίσκεται, μέχρι το σπίτι Μ στην άλλη πλευρά ενός ποταμού. Χρησιμοποιεί ένα γειτονικό σημείο Β που βρίσκεται σε απόσταση ΑΒ = 20 m και με τη βοήθεια ενός γωνιόμετρου βρίσκει ότι

Να υπολογίσετε τις αποστάσεις ΑΗ και ΑΜ.

 8.

Η ακτίνα της Γης είναι R=ΓΑ=6371 km και η γωνία

Να υπολογίσετε με τη βοήθεια του παρακάτω σχήματος την απόσταση

Γης - Σελήνης (ΓΣ).