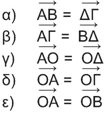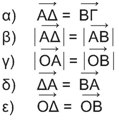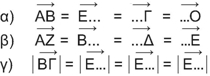Χαρακτηριστικά στοιχεία ενός διανύσματος

Όταν μετράμε ένα μέγεθος, όπως π.χ. το χρόνο που χρειαζόμαστε για να διαβάσουμε αυτή την παράγραφο, γράφουμε τη μέτρηση ως έναν αριθμό που ακολουθείται συνήθως από μία μονάδα μέτρησης. Για παράδειγμα, χρειαζόμαστε 30 δευτερόλεπτα για να διαβάσουμε την παράγραφο αυτή. Χρησιμοποιώντας το σύμβολο t για το χρόνο, γράφουμε: t = 30 (s).

Μερικά μεγέθη προσδιορίζονται πλήρως, αν δοθεί μόνο το μέτρο τους. Για παράδειγμα: ο χρόνος, που εκφράζεται σε ώρες, λεπτά, δευτερόλεπτα κ.τ.λ., η θερμοκρασία που εκφράζεται σε βαθμούς Κελσίου, Φαρενάϊτ κ.τ.λ., η μάζα που εκφράζεται σε χιλιόγραμμα, γραμμάρια κ.τ.λ.

Τέτοια μεγέθη λέγονται βαθμωτά ή μονόμετρα μεγέθη. Όμως, δεν είναι όλα τα μεγέθη μονόμετρα. Υπάρχουν και άλλα, που εκτός από μέτρο έχουν και κατεύθυνση. Ένα παράδειγμα τέτοιου μεγέθους είναι το παρακάτω:

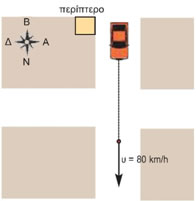
Λύση

Για να προσδιορίσουμε πλήρως την κίνηση του αυτοκινήτου, πρέπει να γνωρίζουμε:

α) Από ποιο σημείο ξεκίνησε το αυτοκίνητο. Στο διπλανό σχήμα φαίνεται ότι ξεκίνησε από το περίπτερο.

β) Προς ποια κατεύθυνση ή αλλιώς με ποια φορά κινείται; Στο σχήμα φαίνεται ότι κινείται νότια.

γ) Το μέτρο της ταχύτητας με την οποία κινείται. Εδώ, το μέτρο της ταχύτητας είναι 80 km/h.

Βλέπουμε, λοιπόν, ότι δεν αρκεί να γνωρίζουμε μόνο το μέτρο της ταχύτητας (80 km/h) αλλά για να καταλάβουμε προς τα πού κινείται το αυτοκίνητο, χρειάζεται η αρχική του θέση και η κατεύθυνσή του.

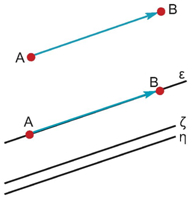
Τα διανυσματικά μεγέθη παριστάνονται με διανύσματα που συμβολίζονται με βέλη έχοντας ένα σημείο Α που είναι η αρχή και λέγεται σημείο εφαρμογής του διανύσματος και ένα σημείο Β που είναι το πέρας (τέλος) του διανύσματος. Το διάνυσμα, τότε, συμβολίζεται με

Ένα διάνυσμα έχει τα εξής στοιχεία:

α) Διεύθυνση, την ευθεία ε που ορίζουν τα άκρα Α, Β ή οποιαδήποτε άλλη ευθεία παράλληλη προς αυτή.

β) Φορά, που καθορίζεται από το αν το διάνυσμα έχει αρχή το Α και πέρας το Β ή αρχή το Β και πέρας το Α

γ) Μέτρο, το μήκος του ευθύγραμμου τμήματος ΑΒ, το οποίο συμβολίζουμε με Το μέτρο είναι πάντοτε ένας αριθμός θετικός ή μηδέν.

Η διεύθυνση μαζί με τη φορά καθορίζουν την κατεύθυνση ενός διανύσματος.

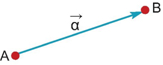
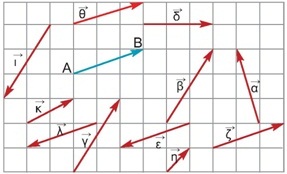
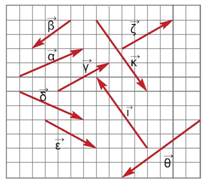
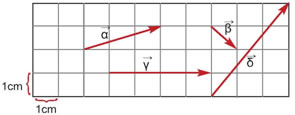
Παρατήρηση:

Συχνά για ευκολία συμβολίζουμε τα διανύσματα με μικρά γράμματα της ελληνικής αλφαβήτου:

Τα διανύσματα παίζουν βασικό ρόλο στη Φυσική. Εκτός από τη μετατόπιση και την ταχύτητα άλλα διανυσματικά μεγέθη είναι η επιτάχυνση, η δύναμη, το βαρυτικό, το ηλεκτρικό, το μαγνητικό πεδίο κ.ά.

Μέτρο διανύσματος

Για να κατανοήσουμε καλύτερα την έννοια του μέτρου του διανύσματος, αρκεί να καταλάβουμε τη διαφορά μεταξύ απόστασης και μετατόπισης. Ας δούμε ένα παράδειγμα:

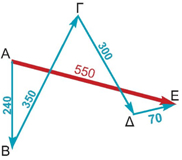
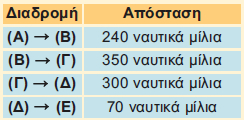
Λύση

Η συνολική απόσταση που διένυσε το πλοίο είναι:

ναυτικά μίλια.

Η απόσταση της αρχικής και τελικής του θέσης είναι:

ναυτικά μίλια.

Η απόσταση είναι βαθμωτό (αριθμητικό) μέγεθος. Λέμε, π.χ. ότι το πλοίο διένυσε απόσταση 960 ναυτικών μιλίων, αλλά δεν ξέρουμε πού πήγε.

Ποια είναι όμως η μετατόπιση του πλοίου;

Η μετατόπιση είναι διανυσματικό μέγεθος. Λέμε, π.χ. ότι το πλοίο ξεκίνησε από τη Σαλαμίνα και μετατοπίστηκε 240 ναυτικά μίλια προς Νότο, οπότε ξέρουμε ακριβώς από πού ξεκίνησε και πού κατέληξε.

Η τελική μετατόπιση του πλοίου εκφράζεται από το διάνυσμα καθώς μας ενδιαφέρει η αρχική και η τελική θέση του πλοίου.

Ας προσέξουμε ιδιαίτερα ότι το μέτρο της μετατόπισης ναυτικά μίλια και δεν έχει καμία σχέση με τη συνολική απόσταση που διένυσε από τη Σαλαμίνα έως το τελευταίο σημείο ανεφοδιασμού (960 ναυτικά μίλια).

Ίσα και αντίθετα διανύσματα

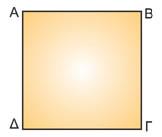
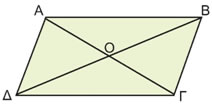
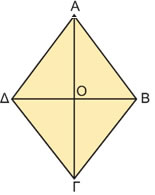
Λύση

Όπως καταλαβαίνουμε τα διανύσματα θα είναι ίσα.

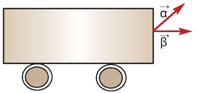
Ας θυμηθούμε ένα παιχνίδι που παίζεται συχνά στις παραλίες ή στις κατασκηνώσεις. Δύο ομάδες παιδιών αρχίζουν να τραβάνε ένα σχοινί προς αντίθετη κατεύθυνση, όπως φαίνεται στο διπλανό σχήμα. Ακριβώς στη μέση του σχοινιού υπάρχει μια γραμμή. Αν μία ομάδα καταφέρει να τραβήξει τον πρώτο παίκτη της άλλης ομάδας μετά τη γραμμή, τότε η ομάδα κερδίζει.

Βλέπουμε ότι οι δυνάμεις που ασκούνται από τις δύο ομάδες, όταν παραμένουν ακίνητες, αλληλοεξουδετερώνονται ή όπως λέμε, είναι αντίθετες.