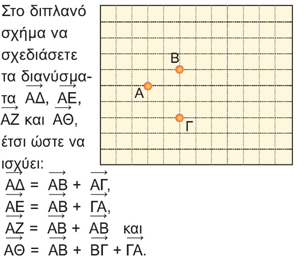
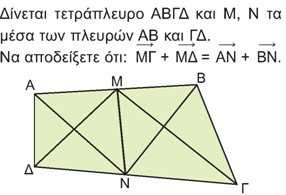
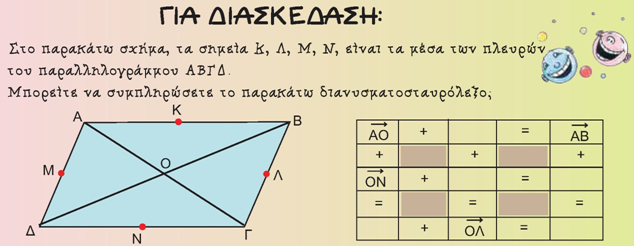
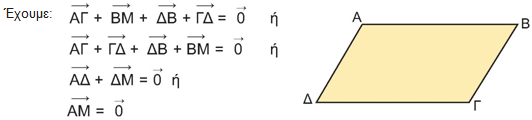| 2.6. | Άθροισμα και διαφορά διανυσμάτων |
|
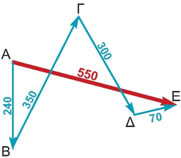
Άθροισμα διανυσμάτωνΣτη δραστηριότητα 2 της προηγούμενης παραγράφου είδαμε ότι η τελική μετατόπιση ήταν το διάνυσμα ΑΕ. Οι διαδοχικές μετατοπίσεις ήταν τα διανύσματα:
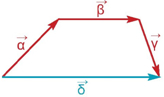
τα οποία λέγονται διαδοχικά διανύσματα, γιατί το τέλος του καθενός είναι η αρχή του επομένου. Είναι φανερό ότι το άθροισμα των διαδοχικών μετατοπίσεων ισούται με την τελική μετατόπιση, δηλαδή:
Με τον τρόπο αυτό ορίζεται το άθροισμα διαδοχικών διανυσμάτων. Τι γίνεται, όμως, όταν τα διανύσματα δεν είναι διαδοχικά; Ας δούμε ένα διαφορετικό παράδειγμα.
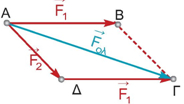
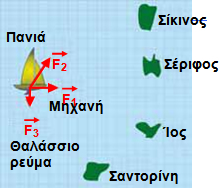
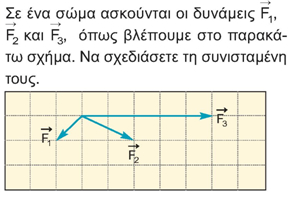
ΛύσηΈχουμε λοιπόν δύο δυνάμεις :
που ασκούνται στο ιστιοπλοϊκό ταυτόχρονα και θέλουμε να βρούμε τη συνισταμένη δύναμη, όπως λέμε στη Φυσική, δηλαδή το άθροισμα των δύο διανυσμάτων :
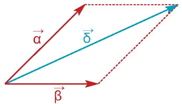
Επομένως, έχουμε δύο μεθόδους, για να βρίσκουμε το άθροισμα διανυσμάτων.
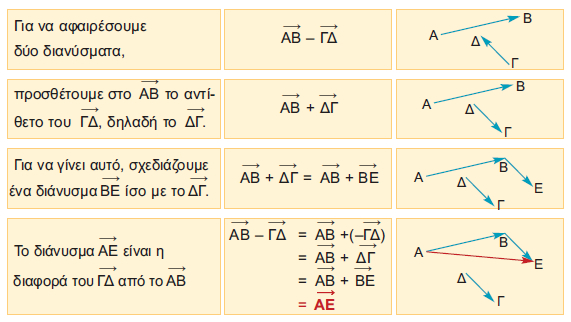
Διαφορά διανυσμάτωνΗ διαφορά δύο διανυσμάτων
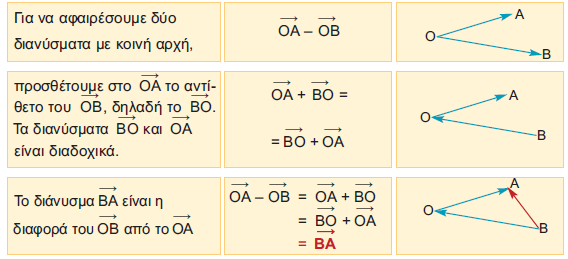
Διαφορά δύο διανυσμάτων με κοινή αρχή
Το μηδενικό διάνυσμαΤο άθροισμα δύο αντίθετων διανυσμάτων είναι ένα διάνυσμα του οποίου η αρχή και το τέλος (πέρας) ταυτίζονται. Το διάνυσμα αυτό λέγεται μηδενικό διάνυσμα και συμβολίζεται με Επομένως, το μηδενικό διάνυσμα είναι ένα σημείο, οπότε δεν έχει ούτε διεύθυνση ούτε φορά. Το μέτρο του είναι ίσο με 0. Δηλαδή: |
||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||