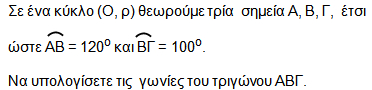
|
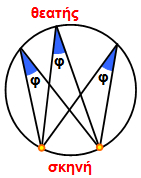
Έχετε αναρωτηθεί ποτέ γιατί τα θέατρα, όπως η Επίδαυρος, έχουν «κυκλικό» σχήμα;
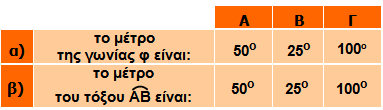
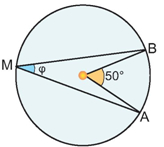
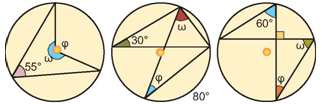
Γιατί από κάθε κάθισμα, που βρίσκεται πάνω στον κύκλο, ο θεατής «βλέπει τη σκηνή με την ίδια γωνία φ».
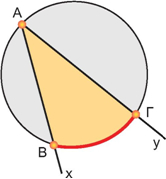
Οι γωνίες που βλέπουμε στο διπλανό σχήμα έχουν την κορυφή τους (θεατής) πάνω στον κύκλο και οι δύο πλευρές τους τέμνουν τον κύκλο. |
 |
Μια γωνία  που η κορυφή της Α ανήκει στον κύκλο (Ο, ρ) και οι πλευρές της Ax, Ay τέμνουν τον κύκλο, λέγεται εγγεγραμμένη γωνία στον κύκλο (Ο, ρ). που η κορυφή της Α ανήκει στον κύκλο (Ο, ρ) και οι πλευρές της Ax, Ay τέμνουν τον κύκλο, λέγεται εγγεγραμμένη γωνία στον κύκλο (Ο, ρ). |
Το τόξο του 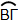 κύκλου (Ο, ρ) που περιέχεται στην εγγεγραμμένη γωνία λέγεται αντίστοιχο τόξο της. κύκλου (Ο, ρ) που περιέχεται στην εγγεγραμμένη γωνία λέγεται αντίστοιχο τόξο της.
Επίσης, λέμε ότι η εγγεγραμμένη γωνία 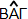 βαίνει στο τόξο βαίνει στο τόξο 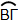 . .
| 1 |
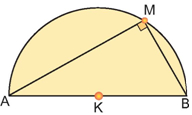
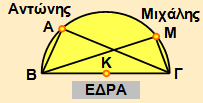
Στο Πανεπιστήμιο γίνεται μάθημα στο Αμφιθέατρο. Δύο φοιτητές, ο Αντώνης και ο Μιχάλης, κάθονται σε μία σειρά θέσεων που σχηματίζει με την έδρα ημικύκλιο, όπως φαίνεται στο παρακάτω σχήμα.
Στο διάλειμμα ο Αντώνης μέτρησε την απόστασή του από τα δύο άκρα Β, Γ της έδρας και βρήκε ότι ΑΒ = 3 m, ΑΓ = 4 m, ενώ έχουμε ότι ΒΓ = 5m. Ο Μιχάλης, αντίστοιχα, βρήκε ότι

α) Να εξετάσετε αν ισχύει το Πυθαγόρειο θεώρημα στα τρίγωνα ΑΒΓ και ΒΜΓ.
β) Τι γωνίες είναι οι  ; ;
γ) Τι συμπεραίνετε γενικά για κάθε εγγεγραμμένη γωνία που βαίνει σε ημικύκλιο;
|
Λύση
α) Έχουμε ότι:
ΑΒ² + ΑΓ² = 3² + 4² = 25 = 5² = ΒΓ²
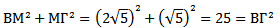
Επομένως, ισχύει το Πυθαγόρειο θεώρημα και στα δύο τρίγωνα ΑΒΓ και ΒΜΓ.
β) Αφού ισχύει το Πυθαγόρειο θεώρημα, θα έχουμε ότι:
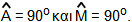
δηλαδή τα τρίγωνα είναι ορθογώνια.
γ) Συμπεραίνουμε ότι η προηγούμενη διαπίστωση ισχύει γενικά, δηλαδή:
Κάθε εγγεγραμμένη γωνία που βαίνει σε ημικύκλιο είναι ορθή. |
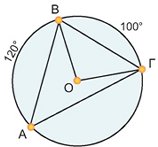
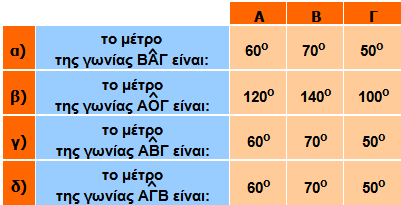
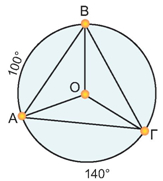
Μια ορθή γωνία που βαίνει σε ημικύκλιο είναι ίση με το μισό της αντίστοιχης επίκεντρης που είναι η πλήρης γωνία. Το συμπέρασμα αυτό ισχύει για κάθε εγγεγραμμένη και την αντίστοιχη επίκεντρη γωνία της.
Συγκεκριμένα
 |
Κάθε εγγεγραμμένη γωνία ισούται με το μισό της επίκεντρης που έχει ίσο αντίστοιχο τόξο. |
 |
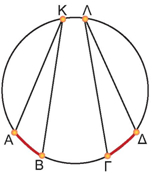
Οι εγγεγραμμένες γωνίες ενός κύκλου που βαίνουν στο ίδιο τόξο ή σε ίσα τόξα είναι μεταξύ τους ίσες. |
 |
Κάθε εγγεγραμμένη γωνία έχει μέτρο ίσο με το μισό του μέτρου του αντίστοιχου τόξου της. |
|