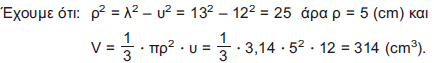4.5. Ο κώνος και τα στοιχεία του

 

 

 

 

 

 

 

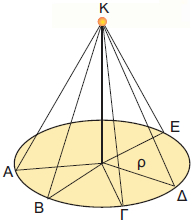
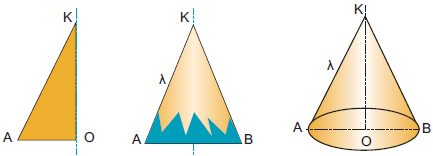
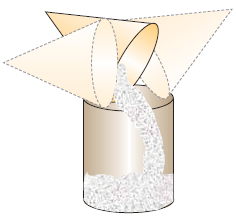
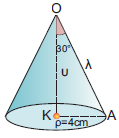
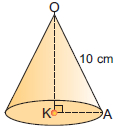
Στην καθημερινή μας ζωή έχουμε συναντήσει συχνά την εικόνα ενός κώνου. Πώς μπορούμε όμως να κατασκευάσουμε προσεγγιστικά ένα κώνο;

Παίρνουμε ένα κυκλικό στεφάνι ακτίνας ρ. Στη συνέχεια, κατασκευάζουμε από χαρτόνι ίσα ορθογώνια τρίγωνα με μια κάθετη πλευρά ίση με την ακτίνα ρ του στεφανιού. Κολλάμε γύρω από ένα ξυλάκι όλα τα ορθογώνια τρίγωνα που κόψαμε, έτσι ώστε να έχουν την ίδια κορυφή Κ και οι βάσεις τους να «πατάνε» στο στεφάνι.

Αν «ντύσουμε» με ύφασμα ή χαρτί το σχήμα που κατασκευάσαμε, τότε εμφανίζεται ένας κώνος.

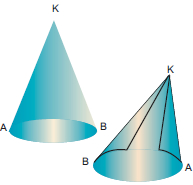
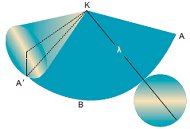
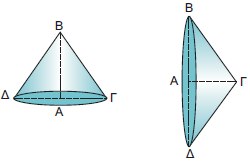
Κώνος λέγεται το στερεό σχήμα που παράγεται από την περιστροφή ενός ορθογωνίου τριγώνου ΚΟΑ γύρω από μία κάθετη πλευρά του ΚΟ.

 

Η βάση του κώνου είναι ένας κυκλικός δίσκος με κέντρο Ο και ακτίνα ΟΑ, την άλλη κάθετη πλευρά του ορθογωνίου ΚΟΑ. Η ακτίνα ΟΑ = ρ λέγεται ακτίνα του κώνου.

Η κάθετη πλευρά ΚΟ γύρω από την οποία περιστρέψαμε το ορθογώνιο τρίγωνο, λέγεται ύψος του κώνου. Η υποτείνουσα ΚΑ του ορθογωνίου τριγώνου λέγεται γενέτειρα του κώνου και το μήκος της συμβολίζεται με λ.

Η επιφάνεια που παράγεται από την περιστροφή τής γενέτειρας ΚΑ είναι η παράπλευρη επιφάνεια του κώνου.

Εμβαδόν επιφάνειας κώνου

Για να υπολογίσουμε το εμβαδόν της παράπλευρης επιφάνειας ΕΠ του κώνου, αρκεί να παρατηρήσουμε ότι το ανάπτυγμά της προκύπτει «ξετυλίγοντας» τον κώνο, όπως φαίνεται στο διπλανό σχήμα.

Παρατηρούμε ότι το ανάπτυγμα της παράπλευρης επιφάνειας του κώνου ισούται με το εμβαδόν ενός κυκλικού τομέα ακτίνας λ με μήκος τόξου

 

To εμβαδόν της παράπλευρης επιφάνειας ενός κώνου είναι ίσο με το εμβαδόν ενός κυκλικού τομέα, που έχει ακτίνα τη γενέτειρα λ του κώνου και μήκος τόξου το μήκος του κύκλου της βάσης του κώνου.

 

 

Για να βρούμε το εμβαδόν της ολικής επιφάνειας του κώνου, αρκεί στο εμβαδόν της παράπλευρης επιφάνειας ΕΠ να προσθέσουμε και το εμβαδόν της βάσης του: EB = πρ2.

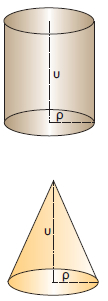
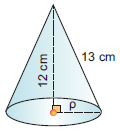
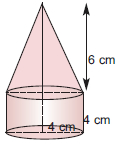
Όγκος κώνου

Κατασκευάζουμε με χαρτόνι ένα κώνο και ένα κύλινδρο, έτσι ώστε να έχουν την ίδια βάση και το ίδιο ύψος. Γνωρίζουμε ότι ο όγκος του κυλίνδρου είναι ίσος με πρ2υ.

Αν γεμίσουμε διαδοχικά με αλεύρι τρεις φορές τον κώνο και αδειάσουμε το αλεύρι μέσα στον κύλινδρο, θα δούμε ότι ο κύλινδρος γεμίζει τελείως.

 

Επομένως, ο όγκος του κώνου είναι το 1/3 του όγκου του κυλίνδρου. Δηλαδή:

1

Nα βρείτε τον όγκο ενός κώνου με γενέτειρα λ = 13 cm και ύψος 12 cm.

 

Λύση:

 

2

H διάμετρος της βάσης ενός κώνου είναι 12 cm και το ύψος του 8 cm. Να υπολογίσετε:

α) το εμβαδόν της παράπλευρης επιφάνειας,

β) τον όγκο του.

 

Λύση:

 

 

3

Στον κώνο του διπλανού σχήματος να υπολογίσετε:

α) το εμβαδόν της ολικής επιφάνειας,

β) τον όγκο του κώνου.

 

Λύση:

 

 

4

Ένας κώνος έχει εμβαδόν παράπλευρης επιφάνειας 251,2 cm2 και γενέτειρα με μήκος 10 cm.

Nα υπολογίσετε: α) την ακτίνα της βάσης του,    β) το ύψος του,    γ) τον όγκο του.

 

Λύση:

 

 
   
ΣΩΣΤΟ ΛΑΘΟΣ

 1.

 To ανάπτυγμα της παράπλευρης επιφάνειας ενός κώνου είναι τρίγωνο.
   

 2.

 Η γενέτειρα λ, το ύψος υ και η ακτίνα ρ του κώνου ικανοποιούν τη σχέση λ2 = υ2 + ρ2.
   

 3.

 Η γενέτειρα ενός κώνου είναι πάντα μεγαλύτερη από την ακτίνα.
   

 4.

 Η βάση ενός κώνου είναι κυκλικός δίσκος.
   

 5.

Η ακτίνα της βάσης ενός κώνου είναι 6 cm και το ύψος του 8 cm. Η γενέτειρά του είναι:

A: 10 dm    B: 10 cm    Γ: 12 m     Δ: 6 cm.

Να κυκλώσετε τη σωστή απάντηση.

 6.

O όγκος του κώνου είναι 12π m3 και η ακτίνα του 3 m. Το ύψος του είναι:

A: π m    B: 6 m    Γ: 4 m    Δ: 4π m.

Να κυκλώσετε τη σωστή απάντηση.

 7.

Αν διπλασιάσουμε την ακτίνα της βάσης ενός κώνου, τότε η παράπλευρη επιφάνεια:

A: διπλασιάζεται    B: τετραπλασιάζεται    Γ: παραμένει ίδια.

Να κυκλώσετε τη σωστή απάντηση.

 8.

Αν διπλασιάσουμε την ακτίνα της βάσης ενός κώνου, τότε ο όγκος του κώνου:

A: διπλασιάζεται   B: τετραπλασιάζεται   Γ: παραμένει ίδιος

Να κυκλώσετε τη σωστή απάντηση.

 9.

Το ανάπτυγμα της παράπλευρης επιφάνειας ενός κώνου είναι κυκλικός τομέας με ακτίνα 12 cm και γωνία 60°. H ακτίνα της βάσης του κώνου είναι:

A: 4 cm    B: 3 dm    Γ: 2 cm    Δ: 2 dm.

Να κυκλώσετε τη σωστή απάντηση.

 10.

Aν διπλασιάσουμε το ύψος ενός κώνου, τότε ο όγκος του:

A: διπλασιάζεται    B: τριπλασιάζεται    Γ: τετραπλασιάζεται.

Να κυκλώσετε τη σωστή απάντηση.

 

 

 1.

Συμπληρώστε τα στοιχεία του κώνου που λείπουν στον παρακάτω πίνακα:

 2.

Ένας κώνος έχει όγκο V = 1 m3.

Να υπολογίσετε τον όγκο του κώνου:

α) με διπλάσιο ύψος (μόνο),

β) με διπλάσια ακτίνα βάσης (μόνο),

γ) με διπλάσιο ύψος και διπλάσια ακτίνα βάσης.

 3.
Ένα δοχείο με σχήμα κώνου που έχει ύψος 20 cm και ακτίνα βάσης 10 cm είναι γεμάτο νερό. Αδειάζουμε το παραπάνω δοχείο σε ένα άλλο δοχείο, που έχει σχήμα κύβου με ακμή 20 cm. Να εξετάσετε αν θα ξεχειλίσει το νερό ή όχι.

 4.
Θέλουμε να κατασκευάσουμε μια κωνική σκηνή, η οποία να έχει όγκο τουλάχιστον 20 m3. Aν το ύψος της σκηνής είναι 3 m, πόση πρέπει να είναι η διάμετρος της βάσης;

 5.
Να υπολογιστεί ο όγκος και το εμβαδόν της ολικής επιφάνειας του στερεού στο διπλανό σχήμα.

 6.
Δύο στερεοί κώνοι έχουν κοινή βάση με ακτίνα 4 cm και ύψη 8 cm και 12 cm αντίστοιχα. Να βρείτε τον όγκο του στερεού που σχηματίζεται.

 7.

Ένα ορθογώνιο τρίγωνο στρέφεται πρώτα γύρω από την πλευρά ΑΒ και έπειτα γύρω από την πλευρά ΑΓ, όπως φαίνεται στα παρακάτω σχήματα.

Να υπολογίσετε:

α) το λόγο των παράπλευρων επιφανειών των δύο κώνων που σχηματίζονται,

β) το λόγο των όγκων τους.

 8.

Ένα ισοσκελές τρίγωνο ΑΒΓ με βάση ΒΓ περιστρέφεται γύρω από τη βάση του ΒΓ, όπως φαίνεται στο παρακάτω σχήμα. Αν ΒΓ=24 cm και AB=13 cm, να υπολογίσετε:

α) την ολική επιφάνεια του στερεού που σχηματίζεται,

β) τον όγκο του.

 9.

Η στέγη της κεντρικής σκηνής ενός τσίρκου έχει σχήμα κώνου με διάμετρο βάσης 40 m και ύψος 15 m. Πόσα τετραγωνικά μέτρα πλαστικοποιημένου υφάσματος χρειάστηκαν για την κατασκευή της;

 10.
Μια κλεψύδρα σχήματος κώνου «μετρά» το χρόνο αδειάζοντας 4 cm3 άμμο το λεπτό (min). Aν η ακτίνα της βάσης είναι 5 cm και το ύψος 9,17 cm, να βρείτε σε πόσο χρόνο θα αδειάσει τελείως η κλεψύδρα;