3.4.	H συνάρτηση y = αx + β

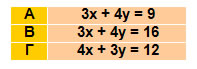
Η ευθεία με εξίσωση y = αx + β

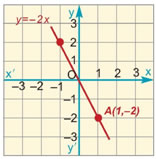
Στις προηγούμενες παραγράφους μάθαμε ότι η γραφική παράσταση της συνάρτησης y = αx είναι ευθεία, η οποία διέρχεται από την αρχή Ο των αξόνων. Σε αυτή την παράγραφο θα μελετήσουμε τη γραφική παράσταση της συνάρτησης y = αx + β. Ας δούμε ένα παράδειγμα:

Το κινητό της Κατερίνας.

Η Κατερίνα έχει κινητό τηλέφωνο με χρέωση 0,9 € για κάθε λεπτό ομιλίας.

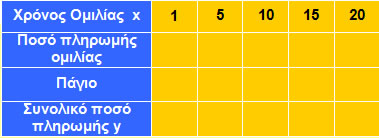
α) Αν ονομάσουμε x το χρόνο ομιλίας (σε λεπτά) και y το ποσό πληρωμής (σε €) που αντιστοιχεί, να συμπληρώσετε τον παρακάτω πίνακα.

Να εκφράσετε το y ως συνάρτηση του x και να σχεδιάσετε σε σύστημα αξόνων τη γραφική παράσταση της συνάρτησης αυτής.

β) Η τηλεφωνική εταιρεία χρεώνει και 10 € πάγιο το μήνα. Να συμπληρώσετε τον παρακάτω πίνακα με το νέο ποσό πληρωμής y με την προσθήκη και των 10 €.

Να εκφράσετε το νέο ποσό πληρωμής y ως συνάρτηση του χρόνου ομιλίας x και να σχεδιάσετε τη γραφική παράσταση της συνάρτησης αυτής στο ίδιο σύστημα συντεταγμένων.

γ) Τι σχέση έχουν οι δύο αυτές γραφικές παραστάσεις;

Λύση

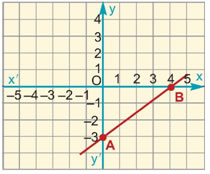
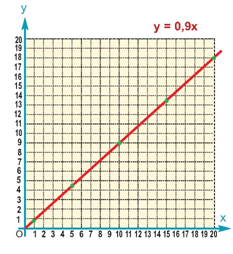
α) Για x = 5 είναι y = 0,9 • 5 = 4,5 €. Ομοίως, βρίσκουμε τα υπόλοιπα ζεύγη του πίνακα.

Παρατηρούμε ότι τα ποσά x και y είναι ανάλογα, γιατί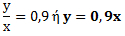

H γραφική παράσταση της συνάρτησης αυτής είναι μια ημιευθεία που αρχίζει από την αρχή των αξόνων και έχει κλίση 0,9, όπως φαίνεται στο διπλανό σχήμα.

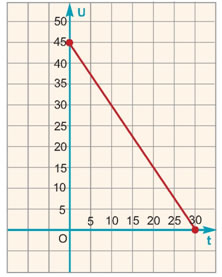
β) Εύκολα συμπληρώνουμε τον πίνακα προσθέτοντας στο ποσό πληρωμής και το πάγιο των 10 €.

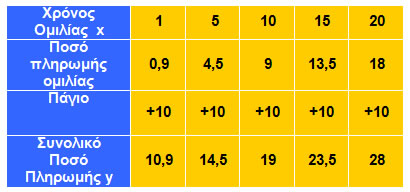
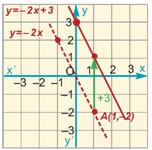
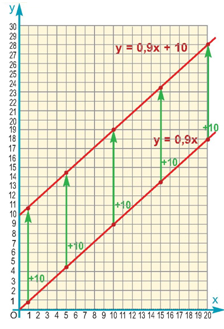
Η νέα συνάρτηση που εκφράζει το συνολικό ποσό πληρωμής είναι y = 0,9x + 10.

Τοποθετούμε στο σύστημα αξόνων τα νέα ζεύγη (x, y) του παραπάνω πίνακα των οποίων η τεταγμένη είναι αυξημένη κατά 10 μονάδες.

Αν ενώσουμε τα νέα αυτά σημεία, παρατηρούμε ότι η γραφική παράσταση της συνάρτησης y = 0,9x + 10 είναι ημιευθεία παράλληλη προς την ημιευθεία y = 0,9x, μετατοπισμένη κατά 10 μονάδες προς τα πάνω στον άξονα y'y.

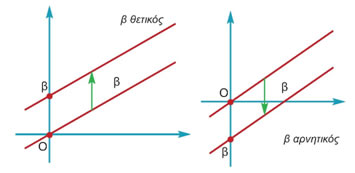
Η γραφική παράσταση της y = αx + β, β≠0 είναι μια ευθεία παράλληλη της ευθείας με εξίσωση

y = αx, που διέρχεται από το σημείο (0, β) του άξονα y'y.

Στο εξής, όταν αναφερόμαστε στην ευθεία που είναι η γραφική παράσταση της συνάρτησης y = αx + β, θα λέμε: η ευθεία με εξίσωση y = αx + β ή απλώς η ευθεία y = αx + β.

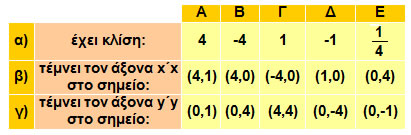
Ο αριθμός α, που, όπως γνωρίζουμε, λέγεται κλίση της ευθείας y = αx, λέγεται και

κλίση της ευθείας y = αx + β.

Η εξίσωση της μορφής αx + βy = γ

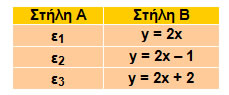
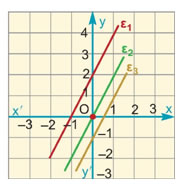
Παρατηρήσαμε ότι οι συναρτήσεις y = αx και y = αx + β παριστάνουν ευθείες. Ωστόσο, υπάρχουν και άλλες εξισώσεις που παριστάνουν ευθείες, όπως φαίνεται στο παρακάτω παράδειγμα.

2
Η κυρία Μαρίκα σκοπεύει να ξοδέψει 15 € για να αγοράσει κρέας που κοστίζει 6 € το κιλό και πατάτες, που κοστίζουν 2 € το κιλό. Ποια σχέση συνδέει τα κιλά κρέας και τα κιλά πατάτες που τελικά θα αγοράσει ;

Λύση

Έστω ότι θα αγοράσει x κιλά κρέας και y κιλά πατάτες. Θα ξοδέψει λοιπόν 6x € για το κρέας και 2y € για πατάτες. Εφόσον διαθέτει μόνο 15 €, πρέπει 6x + 2y = 15.

Αν λύσουμε τη σχέση αυτή ως προς y, έχουμε:

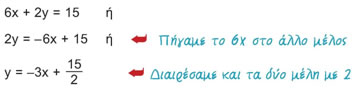
που γνωρίζουμε ότι παριστάνει ευθεία.

Γενικά:

Μια εξίσωση της μορφής αx + βy = γ, με α≠0 ή β≠0 παριστάνει ευθεία.

Για παράδειγμα:

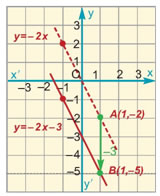
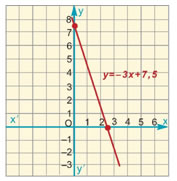
Η εξίσωση 12x + 3y = 15 γράφεται 3y = –12x + 15 ή y = –4x + 5 και παριστάνει ευθεία με κλίση α = –4.

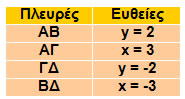
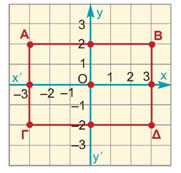
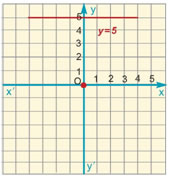
Η εξίσωση 0x + 3y = 15 γράφεται y = 5 και παριστάνει ευθεία παράλληλη προς τον άξονα x'x.

Γενικότερα, η εξίσωση y = κ παριστάνει ευθεία παράλληλη προς τον άξονα x'x.

Η ευθεία y = 0 παριστάνει τον άξονα x'x.

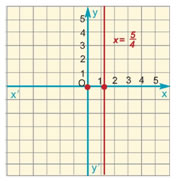
Η εξίσωση 12x + 0y = 15 γράφεται

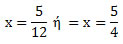
και παριστάνει ευθεία παράλληλη προς τον άξονα y'y.

Γενικότερα, η εξίσωση x = κ, παριστάνει ευθεία παράλληλη προς τον άξονα y'y.

Η ευθεία x = 0 παριστάνει τον άξονα y'y.

Σημεία τομής της ευθείας αx + βy = γ με τους άξονες

Γνωρίζουμε ότι ο άξονας x'x έχει εξίσωση y = 0.

Επομένως, για να βρούμε το σημείο Α στο οποίο η ευθεία αx + βy = γ, με α ≠ 0 ή β ≠ 0 τέμνει τον άξονα x'x, θέτουμε y = 0 και υπολογίζουμε την τετμημένη του x.

Γνωρίζουμε ότι ο άξονας y'y έχει εξίσωση x = 0.

Επομένως, για να βρούμε το σημείο Β στο οποίο η ευθεία αx + βy = γ, με α≠0 ή β≠0 τέμνει τον άξονα y'y, θέτουμε x = 0 και υπολογίζουμε την τεταγμένη του y.

1
Να σχεδιάσετε τις γραφικές παραστάσεις των συναρτήσεων y = –2x, y = –2x + 3 και y = –2x –3, όπου x ο πραγματικός αριθμός.

Λύση:

H γραφική παράσταση της συνάρτησης y = –2x είναι ευθεία, η οποία διέρχεται από την αρχή Ο των αξόνων. Για να τη σχεδιάσουμε, αρκεί να βρούμε ένα ακόμη σημείο της.

Για x = 1 είναι y = –2 • 1 = –2.

Άρα, διέρχεται και από το σημείο Α με συντεταγμένες (1,–2). Ενώνουμε το Ο με το Α και προεκτείνουμε.

Η γραφική παράσταση της y = –2x φαίνεται στο διπλανό σχήμα.

Η γραφική παράσταση της συνάρτησης y = –2x + 3 είναι ευθεία παράλληλη με την y = –2x και τέμνει τον άξονα y'y στο σημείο (0, 3).

Μεταφέρουμε το σημείο (0, 0) στο σημείο (0, 3) και το σημείο (1, –2) στο

(1, 1).

Ενώνουμε τα νέα αυτά σημεία και προεκτείνουμε.

Η γραφική παράσταση της συνάρτησης y = –2x + 3 φαίνεται στο διπλανό σχήμα.

Ομοίως, η γραφική παράσταση της συνάρτησης y = –2χ – 3 είναι ευθεία παράλληλη με την y = –2x και τέμνει τον άξονα y'y στο σημείο (0, –3). Μεταφέρουμε το σημείο (0, 0) στο σημείο (0, –3) και το σημείο (1, –2) στο

(1, –5).

Ενώνουμε τα σημεία αυτά και προεκτείνουμε, όπως φαίνεται στο διπλανό σχήμα.

Δίνεται η εξίσωση 3x – 4y = 12, όπου x, y πραγματικοί αριθμοί.

α) Να βρείτε τα σημεία στα οποία η ευθεία αυτή τέμνει τους άξονες.

β) Να τη σχεδιάσετε σε σύστημα αξόνων.

γ) Να εκφράσετε το y ως συνάρτηση του x και να βρείτε την κλίση της ευθείας.

Λύση:

α) Για τον άξονα y΄y:

θέτουμε x = 0 στην εξίσωση της ευθείας, οπότε έχουμε:

3 • 0 – 4y = 12 ή – 4y =12 ή

Άρα, τέμνει τον άξονα y΄y στο σημείο Α με συντεταγμένες (0, – 3).

Για τον άξονα x΄x:

θέτουμε y = 0 στην εξίσωση της ευθείας, οπότε έχουμε:

3 • x – 4 • 0 = 12 ή 3x = 12 ή

Άρα, τέμνει τον άξονα x΄x στο σημείο Β με συντεταγμένες (4, 0).

β) Ενώνουμε τα παραπάνω σημεία Α και Β και προεκτείνουμε.

Η γραφική παράσταση της ευθείας 3x – 4y = 12 φαίνεται στο διπλανό σχήμα.

γ) Για να εκφράσουμε το y ως συνάρτηση του x, λύνουμε ως προς y τη σχέση 3x – 4y = 12,

δηλαδή:

Η κλίση της ευθείας αυτής είναι

Η προσγείωση ενός αεροπλάνου

Η ταχύτητα (σε m/s) ενος αεροπλανου που προσγειώνεται, από τη στιγμή που αγγίζει το έδαφος μέχρι να σταματήσει, δίνεται από τη σχέση: υ = 45 – 1,5 t, όπου t ο χρόνος που πέρασε από τη χρονική στιγμή που το αεροπλάνο άγγιξε το έδαφος.

α) Να βρείτε την ταχύτητά του τη στιγμή που αγγίζει το έδαφος.

β) Να βρείτε το χρόνο που απαιτείται για να σταματήσει το αεροπλάνο και να παραστήσετε γραφικά την ταχύτητά του υ ως συνάρτηση του χρόνου t.

Λύση:

α) Για t = 0 η ισότητα υ = 45 – 1,5 t δίνει υ = 45 m/s.

β)Τη στιγμή που σταματάει, το αεροπλάνο έχει ταχύτητα 0 m/s.

Για την τιμή αυτή του υ, η ισότητα υ = 45 – 1,5 t γίνεται:

0 = 45 – 1,5 t

1,5 t = 45

t = 30 (s).

Άρα, οι δυνατές τιμές του χρόνου t είναι 0 ≤ t ≤ 30.

Η γραφική παράσταση της συνάρτησης υ = 45 – 1,5 t είναι ευθύγραμμο τμήμα

με άκρα τα σημεία (0, 45) και (30, 0).

1.	H ευθεία y = 3x είναι παράλληλη προς την: Nα επιλέξετε τη σωστή απάντηση.
2.	Στο διπλανό σχήμα έχουμε σχεδιάσει τις τρεις παράλληλες ευθείες της στήλης Β. Να αντιστοιχίσετε καθεμιά με την εξίσωσή της.
3.	Στο διπλανό σχήμα το ορθογώνιο ΑΒΓΔ έχει κέντρο το Ο και οι πλευρές του είναι παράλληλες προς τους άξονες x'x και y'y. Να αντιστοιχίσετε κάθε πλευρά με την εξίσωση της ευθείας στην οποία ανήκει.
4.	Η ευθεία με εξίσωση 4x + y = 4 Nα επιλέξετε τη σωστή απάντηση.
5.	Μια ευθεία ε τέμνει τους άξονες στα σημεία (3, 0) και (0, 4). Η εξίσωσή της είναι: Nα επιλέξετε τη σωστή απάντηση.

1.	Στο ίδιο σύστημα ορθογωνίων αξόνων να παραστήσετε γραφικά τις ευθείες με εξισώσεις:
2.	Να παραστήσετε γραφικά τη συνάρτηση y = –3x + 2, όταν: α) ο x είναι πραγματικός αριθμός. β) x ≥ 0. γ) –2 ≤ x ≤ 5.
3.	Να βρείτε την εξίσωση της ευθείας η οποία έχει κλίση 2 και τέμνει τον άξονα y'y στο σημείο με τεταγμένη –3.
4.	Στο σχήμα δίνονται τα σημεία Α(1, 1) και Β(2, 3). α) Να αποδείξετε ότι η απόσταση ΑΒ είναι ίση με β) Να αποδείξετε ότι η ευθεία με εξίσωση y = 2x – 1 διέρχεται από τα σημεία Α και Β.
5.	Όταν χρησιμοποιούμε ταξί, πληρώνουμε 0,5 € για τη σημαία και 0,2 € για κάθε χιλιόμετρο διαδρομής. Να βρείτε τη συνάρτηση που μας δίνει το ποσό y που θα πληρώσουμε για μια διαδρομή x χιλιομέτρων.
6.	Δίνεται η ευθεία με εξίσωση 2x – 3y = 6. Να βρείτε τα σημεία στα οποία τέμνει τους άξονες.
7.	Να σχεδιάσετε τη γραφική παράσταση της ευθείας x + y = 2.

Να σχεδιάσετε στο ίδιο σύστημα ορθογωνίων αξόνων το ορθογώνιο ΑΒΓΔ, του οποίου οι πλευρές ανήκουν στις ευθείες y = 2, y = 3, x = 1 και x = –2.

Ποιες είναι οι συντεταγμένες των κορυφών Α, Β, Γ και Δ;

Ποιο είναι το εμβαδόν του ορθογωνίου ΑΒΓΔ;

Ένα εργοστάσιο κατασκευάζει ηλεκτρονικούς υπολογιστές με κόστος 200 € το τεμάχιο. Επίσης, πληρώνει 100 € την ημέρα για την ενοικίαση μιας αποθήκης, για να αποθηκεύει τους ηλεκτρονικούς υπολογιστές.

α) Να εκφράσετε το συνολικό ημερήσιο κόστος y του εργοστασίου ως συνάρτηση του αριθμού x των ηλεκτρονικών υπολογιστών που κατασκευάζει ημερησίως.

β) Να σχεδιάσετε σε σύστημα ορθογωνίων αξόνων τη συνάρτηση αυτή.

10.

Σε ένα τηλεοπτικό παιχνίδι κάθε παίκτης ξεκινάει έχοντας ως δώρο από την εταιρεία παραγωγής 1000 €. Στη συνέχεια, πρέπει να απαντήσει σε 20 ερωτήσεις. Σε κάθε σωστή απάντηση κερδίζει 100 €, ενώ σε κάθε λανθασμένη απάντηση χάνει 50 €. Συμβολίζουμε με x το πλήθος των σωστών απαντήσεων.

α) Να εκφράσετε ως συνάρτηση του x το πλήθος ω των λανθασμένων απαντήσεων.

β) Να εκφράσετε ως συνάρτηση του x το συνολικό κέρδος y του παίκτη.

γ) Να παραστήσετε γραφικά τη συνάρτηση y.