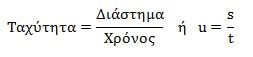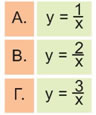| 3.5. |
|
Ποσά αντιστρόφως ανάλογα - Η υπερβολήΌπως γνωρίζουμε από τη Φυσική, όταν ένα σώμα κινείται, η ταχύτητά του δίνεται από τη σχέση:
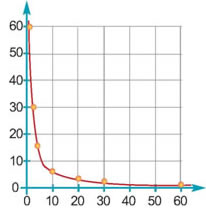
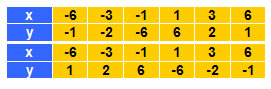
Λύσηα) Συμπληρώνουμε τον πίνακα:
Παρατηρούμε ότι το γινόμενο υ • t παριστάνει την απόσταση s και είναι πάντοτε 60, δηλαδή υ • t = 60.
β) Τα ποσά υ και t, όπως είδαμε και σε προηγούμενες τάξεις, λέγονται αντιστρόφως ανάλογα, γιατί όταν η τιμή του ενός πολλαπλασιαστεί επί έναν αριθμό, τότε η τιμή του άλλου διαιρείται με τον αριθμό αυτό. Το γινόμενο υ • t των ποσών υ και t, αν είναι αντιστρόφως ανάλογα, είναι σταθερό.
γ) Σε σύστημα συντεταγμένων τοποθετούμε όλα τα σημεία που έχουν συντεταγμένες τα ζεύγη (t,υ) του παραπάνω πίνακα. Mια πρόχειρη γραφική παράσταση της συνάρτησης, φαίνεται στο διπλανό σχήμα.
Σε δύο ανάλογα ποσά x και y, οι τιμές τους μπορεί να είναι και αρνητικοί αριθμοί.
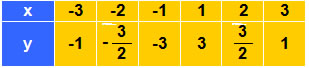
Λύσηα) Συμπληρώνουμε τον πίνακα:
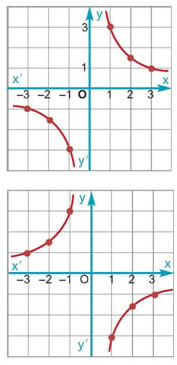
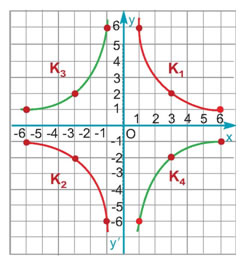
Σε σύστημα συντεταγμένων τοποθετούμε τα σημεία που έχουν συντεταγμένες τα ζεύγη τιμών (x, y) του παραπάνω πίνακα. Τα σημεία αυτά σχηματίζουν δύο γραμμές, μία στο πρώτο τεταρτημόριο και μία στο τρίτο, όπως στο διπλανό σχήμα.
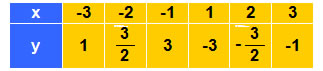
β) Σχηματίζουμε τον παρακάτω πίνακα τιμών:
Τα σημεία αυτά σχηματίζουν δύο γραμμές, μία στο δεύτερο τεταρτημόριο και μία στο τέταρτο τεταρτημόριο, όπως στο διπλανό σχήμα.
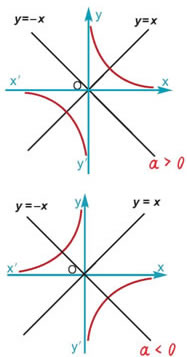
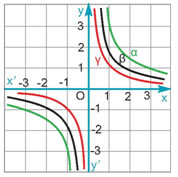
Γενικά:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||