3.1. H έννοια της συνάρτησης

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
1

Κατά καιρούς ακούμε στην τηλεόραση για τις αυξήσεις στους μισθούς των εργαζομένων.

Αυτή τη χρονιά ανακοινώθηκε αύξηση 3%.

α) Δύο εργαζόμενοι έχουν μισθούς 800 € και 1100 € το μήνα. Πόση είναι η αύξηση που θα πάρει ο καθένας;

β) Ένας εργαζόμενος έχει μισθό x €. Ποια είναι η αύξηση y που θα πάρει εφέτος;

Λύση

α) Η αύξηση θα είναι:

     για τον πρώτο εργαζόμενο:

     για τον δεύτερο εργαζόμενο:

β) Η αύξηση θα είναι:

 

Παρατήρηση:

H σχέση y = 0,03x μπορεί να χρησιμοποιηθεί και για άλλες τιμές της μεταβλητής x.

Αν, για παράδειγμα, ένας εργαζόμενος έχει μισθό x = 700 €, η αύξηση που θα πάρει θα είναι y = 0,03 • 700 = 21 €.

Ομοίως, για x = 1500 βρίσκουμε αύξηση y = 0,03 • 1500 = 45 €.

 

Με τη σχέση αυτή κάθε τιμή της μεταβλητής x (παλιός μισθός), αντιστοιχίζεται σε μία μόνο τιμή της μεταβλητής y (αύξηση).

Μια τέτοια σχέση στα Μαθηματικά λέγεται συνάρτηση.

 

Στην περίπτωση αυτή λέμε ότι «η μεταβλητή y εκφράζεται ως συνάρτηση της μεταβλητής x». Έτσι, μπορούμε να λέμε απλά ότι έχουμε ορίσει τη συνάρτηση y = 0,03x.

 

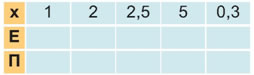
Πίνακας Τιμών

Η αντιστοιχία μεταξύ των τιμών των μεταβλητών x και y φαίνεται καλύτερα με τη βοήθεια του πίνακα τιμών.

Έτσι, για τη συνάρτηση y = 0,03x έχουμε:

Για x = 700, y = 0,03 • 700 = 21.
Για x = 800, y = 0,03 • 800 = 24.
Για x = 900, y = 0,03 • 900 = 27.
Για x = 1000, y = 0,03 • 1000 = 30.
Για x = 1100, y = 0,03 • 1100 = 33.

 

Τα ζεύγη των τιμών αυτών παρουσιάζονται στον διπλανό πίνακα, o οποίος λέγεται πίνακας τιμών της συνάρτησης y = 0,03x.

 

 

1

Δίνεται η συνάρτηση y = 2x + 3. Να συμπληρώσετε τον παρακάτω πίνακα τιμών:

 

Λύση:
Για x = -2: y = 2 • (-2) + 3 = -4 + 3 = -1.
Για x = -1: y = 2 • (-1) + 3 = -2 + 3 = 1.
Για x = 0: y = 2 • 0 + 3 = 3.
Για x = 1: y = 2 • 1 + 3 = 2 + 3 = 5.
Για x = 2: y = 2 • 2 + 3 = 4 + 3 = 7.
Άρα, ο πίνακας τιμών είναι:

 

 

2

Ένας ελαιοπαραγωγός έχει υπολογίσει ότι από κάθε κιλό ελιάς που πηγαίνει στο ελαιοτριβείο, παίρνει 0,2 κιλά λάδι.

α) Πόσα κιλά λάδι θα πάρει από παραγωγή 500 κιλών ελιών;

β) Να εκφράσετε την ποσότητα y σε κιλά του λαδιού, που θα πάρει, ως συνάρτηση της ποσότητας x των ελιών που παράγει.

γ) Πόσα κιλά ελιές πρέπει να παράγει, ώστε να πάρει 250 κιλά λάδι;

 

Λύση:

α) Αφού από 1 κιλό ελιές παίρνει 0,2 κιλά λάδι, από 500 κιλά ελιές θα πάρει 0,2 • 500 = 100 κιλά λάδι.

β) Από x κιλά ελιές θα πάρει 0,2x κιλά λάδι. Δηλαδή y = 0,2x.

γ) Από τη συνάρτηση y = 0,2x, για y = 250 κιλά λάδι έχουμε: 250 = 0,2x

ή

Άρα, θα πρέπει να παράγει 1250 κιλά ελιές.

 

 

 1.

O! μισθοί των υπαλλήλων μιας εταιρείας αυξάνονται κατά 20 € ο καθένας. Η σχέση που εκφράζει το νέο μισθό y ως συνάρτηση του παλιού μισθού x, είναι:

 2.

Οι μισθοί των υπαλλήλων μιας εταιρείας αυξάνονται κατά 15%. Η σχέση που εκφράζει το νέο μισθό y ως συνάρτηση του παλιού μισθού x, είναι:

 3.

Το εμβαδόν ενός ορθογωνίου με πλευρές x και y είναι . H σχέση που εκφράζει το μήκος του y ως συνάρτηση του x, είναι:

 4.

Δίνεται τετράγωνο πλευράς x. Η σχέση που εκφράζει το εμβαδόν E του τετραγώνου ως συνάρτηση του x είναι:

 5.

Να αντιστοιχίσετε τις συναρτήσεις της στήλης Α του διπλανού πίνακα με τον πίνακα τιμών της στήλης Β.

(Στη στήλη Β ένας πίνακας τιμών περισσεύει.)

 

 

 1.

Nα συμπληρώσετε τον πίνακα τιμών των παρακάτω συναρτήσεων:

 2.

Nα συμπληρώσετε τον πίνακα τιμών των παρακάτω συναρτήσεων:

 

 3.

Οι τιμές ενός καταστήματος ηλεκτρονικών επιβαρύνονται με φόρο 8%.

Να εκφράσετε τις τιμές y με φόρο, ως συνάρτηση των τιμών x χωρίς φόρο.

 4.

Ένας πωλητής παίρνει μισθό 600 € το μήνα και ποσοστό 7% επί του ποσού των πωλήσεων που πραγματοποιεί.

Να εκφράσετε το συνολικό ποσό y, που κερδίζει το μήνα, ως συνάρτηση του ποσού x των πωλήσεων που πραγματοποιεί

 5.

Ένα ορθογώνιο έχει πλευρές με μήκη x και y (σε cm).

α)Αν η περίμετρος του ορθογωνίου είναι 60 cm, να εκφράσετε την πλευρά y ως συνάρτηση της πλευράς x.

 

β) Αν το εμβαδόν του ορθογωνίου είναι , να εκφράσετε την πλευρά y ως συνάρτηση της πλευράς x.

 6.

Ένα τετράγωνο έχει πλευρά με μήκος x (σε cm). Να εκφράσετε το εμβαδόν Ε και την περίμετρο Π του τετραγώνου ως συναρτήσεις του x. Στη συνέχεια, να συμπληρώσετε τον πίνακα τιμών:

 

 7.

Να συμπληρώσετε τον παρακάτω πίνακα τιμών της συνάρτησης y = 3x - 5:

 

 8.

Ένα αυτοκίνητο κινείται με ταχύτητα 70 χιλιόμετρα την ώρα.

α) Πόση απόσταση θα έχει διανύσει σε 2 ώρες και πόση σε 5 ημέρες;

β) Να εκφράσετε την απόσταση S (σε χιλιόμετρα) που θα έχει διανύσει το αυτοκίνητο ως συνάρτηση του χρόνου t (σε ώρες).